الگوریتم دایجسترا

نام این الگوریتم بر اساس نام ارائه‌دهنده هلندی آن، یعنی اِدسخِر دایکسترا انتخاب شده‌است. در منابع فارسی آن را به شکل‌های دِیکسترا، دکسترا، دایکسترا، دایجسترا، دیجسترا، دایجکسترا و دیجکسترا هم نوشته شده است، ولی جیمِ آن در تلفظ هلندی آن تلفظ نمی‌شود، لذا دو مورد اول صحیح‌ هستند.

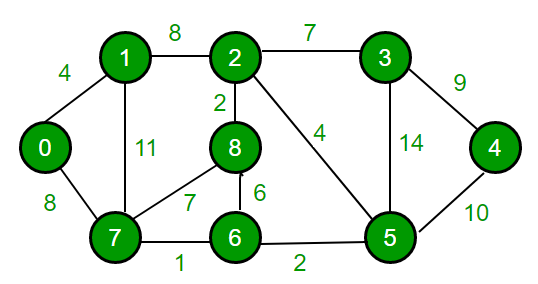
الگوریتم دایجسترا راه‌کاری برای پیدا کردن کم‌وزن مسیر از رأس مشخص آغاز به بقیه رئوس در گراف جهت‌دار و وزن‌دار (با وزن‌های مثبت) می‌دهد. وزن یک مسیر در گراف وزن‌دار برابر مجموع وزن یال‌های آن است. جهت‌دار نبودن یال‌ها هم مشکلی ایجاد نمی‌کند و می‌توان برای یال‌های غیر جهت‌دار دو یال فرض کرد.

لگوریتم

فرض کنید 1≤‌s≤n که در آن رأس ‌s رأس آغاز است و فرض کنید:

dist(r)=0

و به ازای هر v≠r:

dist(v)=∞

فرض کنید مجموعه‌ی T برابر رئوسی باشد که تا کنون کم وزن‌ترین مسیر آن‌ها را پیدا کرده‌ایم. این الگوریتم در هر مرحله نزدیک‌ترین رأس به s را که تا کنون به مجموعه‌ی ‌T اضافه نشده را انتخاب می‌کند (مثلا ‌x) و آن را به مجموعه‌ی T اضافه می‌کند و فاصله‌ی دیگر رأس‌ها را با توجه به فاصله‌‌ی x بروز می‌کند. به ازای هر رأس v خارج T:....

dist(v)=min(dist(v),dist(x)+w(x,v))

که در آن w(x,v) برابر وزن یال بین x و v است. این الگوریتم در هر مرحله رأسی را که کوتاه‌ترین فاصله‌ی آن تا s پیدا شده‌ است را به T اضافه می‌کند. زیرا کوتاه ترین مسیر این رأس از یکی از رأس‌های T می‌گذرد که در مراحل قبلی فاصله آن‌ها بدست آمده و دیگر رئوس را بروز کرده‌اند.

در نظریه گراف، الگوریتم دیکسترا (به انگلیسی: Dijkstra's algorithm) یکی از الگوریتم‌های پیمایش گراف است که توسط دانشمند هلندی علوم رایانه، اِدْسْخِر دیْکْسْترا در سال ۱۹۵۹ ارائه شد.

این الگوریتم یکی از الگوریتم‌های پیمایش گراف است که مسئلهٔ کوتاه‌ترین مسیر از مبدأ واحد را برای گراف‌های وزن‌داری که یال با وزن منفی ندارند، حل می‌کند و در نهایت با ایجاد درخت کوتاه‌ترین مسیر، کوتاه‌ترین مسیر از مبدأ به همهٔ رأس‌های گراف را به دست می‌دهد. همچنین می‌توان از این الگوریتم برای پیدا کردن کوتاه‌ترین مسیر از مبدأ تا رأس مقصد به این ترتیب بهره جست که در حین اجرای الگوریتم به محض پیداشدن کوتاه‌ترین مسیر از مبدأ به مقصد، الگوریتم را متوقف کرد.

الگوریتم دیکسترا یکی از الگوریتم‌های مورد استفاده برای محاسبه کوتاه‌ترین مسیر تک منبع (single-source shortest path) است و مشابه الگوریتم پریم می‌باشد در صورتی که گراف یال با وزن منفی داشته باشد، این الگوریتم درست کار نمی‌کند و می‌بایست از الگوریتم‌های دیگر نظیر الگوریتم بلمن-فورد که پیچیدگی زمانی آن‌ها بیشتر است استفاده کنیم.

خط مشی الگوریتم دیکسترا، مشابه با روش حریصانهٔ استفاده شده در الگوریتم پریم برای پیدا کردن زیر درخت فراگیر بهینه است.

روند الگوریتم دایکسترا مطابق زیر می‌باشد:

۱- انتخاب راس مبدا

پیمایش گراف و پیمایش درخت

هرس آلفا بتا

A*

B*

Beam

الگوریتم بلمن–فورد

جستجوی ابتدا بهترین

جستجوی دوجهته

الگوریتم جستجوی اول سطح

D*

الگوریتم جستجوی عمق اول

جستجوی عمق محدود

الگوریتم دیکسترا

الگوریتم فلوید-وارشال

الگوریتم تپه‌نوردی

جستجوی عمق اول عمیق‌کننده تکراری

الگوریتم جانسون

Lexicographic breadth-first

Uniform-cost

رده:الگوریتم‌های جستجو

جستار وابسته

برنامه‌ریزی پویا

Search games

۲- مجموعهٔ S، شامل رئوس گراف، معین می‌شود. در شروع، این مجموعه تهی بوده و با پیشرفت الگوریتم، این مجموعه رئوسی که کوتاه‌ترین مسیر به آن‌ها یافت شده‌است را در بر می‌گیرد.

۳- راس مبدأ با اندیس صفر را در داخل S قرار می‌دهد.

۴- برای رئوس خارج از S، اندیسی معادل، طول یال + اندیس راس قبلی، در نظر می‌گیرد. اگر راس خارج از مجموعه دارای اندیس باشد، اندیس جدید کمترین مقدار از بین اندیس قبلی و طول یال + اندیس راس قبل، می‌باشد.

۵- از رئوس خارج مجموعه، راسی با کمترین اندیس انتخاب شده و به مجموعهٔ S اضافه می‌گردد.

۶- این کار را دوباره از مرحلهٔ ۴ ادامه داده تا راس مقصد وارد مجموعهٔ S شود.

در پایان اگر راس مقصد دارای اندیس باشد، اندیس آن نشان دهندهٔ مسافت بین مبدأ و مقصد می‌باشد. در غیر این صورت هیچ مسیری بین مبدأ و مقصد موجود نمی‌باشد.

همچنین برای پیدا کردن مسیر می‌توان اندیس دیگری برای هر راس در نظر گرفت که نشان دهندهٔ راس قبلی در مسیر طی شده باشد. بدین ترتیب پس از پایان اجرای الگوریتم، با دنبال کردن رئوس قبلی از مقصد به مبدا، کوتاه‌ترین مسیر بین دو نقطه نیز یافت می‌شود.

هدف

در حین اجرای الگوریتم دو چیز به‌طور ضمنی نگهداری می‌شود. یکی مجموعهٔ  از رأس‌هایی که وزن کوتاه‌ترین مسیر از مبدأ تا آن‌ها مشخص شده و دیگری دنبالهٔ  که برای هر رأس ، مقدار  برابر وزن کوتاه‌ترین مسیر از مبدأ تا  است به شرطی که تمام رأس‌های این مسیر به جز  از رئوس داخل  باشند.  در ابتدا تهی و مقادیر  برای همهٔ رئوس به غیر از مبدأ بی‌نهایت است و مقدار آن برای مبدأ صفر گذاشته می‌شود. الگوریتم در هر مرحله رأسی خارج  را که  برای آن کمترین است انتخاب و به مجموعهٔ  اضافه می‌کند و سپس مقادیر  را برای رئوس همسایهٔ آن رأس به‌روز می‌نماید. در صورتی که نیاز به تشکیل درخت کوتاه‌ترین مسیر باشد، الگوریتم می‌بایست دنبالهٔ  را که  پدر رأس  در درخت کوتاه‌ترین مسیر است، به همراه دنبالهٔ  به‌روز کند.

کاربردها

از جمله مهمترین کاربردهای این روش می‌توان به محاسبهٔ کوتاه‌ترین فاصلهٔ دو نقطه در یک شهر از طریق راه‌های زمینی اشاره نمود. برای محاسبهٔ کوتاه‌ترین مسیر بین دو نقطه باید نقاط مورد نظر در یک نقشه را علامت گذاری کرد و با استفاده از مشخصات نقاط (طول، عرض و ارتفاع) فاصلهٔ دو نقطه را در هر بار عملیات محاسبه نمود. توجه داریم که در ترافیک سرعت خودروها به شدت پایین آمده و این امر می‌تواند در انتخاب کوتاه‌ترین مسیر تأثیر گذار باشد چرا که ممکن است بین دو نقطه a,b راه‌های ۱و۲ موجود باشد که راه ۱ اتوبان و از خارج شهر و راه ۲ از داخل شهر عبور می‌کند. فرض کنید فاصلهٔ a,b از طریق راه ۱ حدود ۱۰ کیلومتر و از طریق راه ۲ حدود ۷ کیلومتر باشد ولی راه ۲ علی رقم فاصلهٔ کمتر دارای ترافیک سنگین است در نتیجه می‌توان انتظار داشت که در ساعات شلوغی استفاده از راه ۱ بهتر باشد. از آن جا که اساس محاسبات در این روش بر پایهٔ فاصله بین دو نقطه است می‌توان کاهش سرعت را با افزایش فواصل هم ارز نمود چرا که اگر رابطهٔ سرعت و فاصله را خطی در نظر بگیریم (D=V.T)تاثیر کاهش سرعت و افزایش مسافت یکسان است. از این رو لازم است تا ضرایب تعدیلی در فواصل بین نقاط ضرب شده و این مسائل را در محاسبات لحاظ کرد. از جمله مهم‌ترین این ضرایب می‌توان به ۳ مورد زیر اشاره نمود: ۱-ضریب ترافیک و شلوغی ۲-ضریب عرض معبر ۳-ضریب شیب که نشانگر افت سرعت در سر بالایی هااست. گرچه تعیین این ضرایب برای نقاط مختلف شهر نیازمند کارشناسان متخصص ترافیک و بررسی‌های آماری دقیق می‌باشد ولی می‌توان انتظار داشت که در اکثر موارد این ضرایب بین مقادیر ۱ تا ۲ بسته به شرایط تغییر کنند

نمونه و مثال

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;

namespace DijkstraAlgorithm
{
    class Dijkstra
    {

        private static int MinimumDistance(int[] distance, bool[] shortestPathTreeSet, int verticesCount)
        {
            int min = int.MaxValue;
            int minIndex = 0;

            for (int v = 0; v < verticesCount; ++v)
            {
                if (shortestPathTreeSet[v] == false && distance[v] <= min)
                {
                    min = distance[v];
                    minIndex = v;
                }
            }

            return minIndex;
        }

        private static void Print(int[] distance, int verticesCount)
        {
            Console.WriteLine("Vertex    Distance from source");

            for (int i = 0; i < verticesCount; ++i)
                Console.WriteLine("{0}\t  {1}", i, distance[i]);
        }

        public static void DijkstraAlgo(int[,] graph, int source, int verticesCount)
        {
            int[] distance = new int[verticesCount];
            bool[] shortestPathTreeSet = new bool[verticesCount];

            for (int i = 0; i < verticesCount; ++i)
            {
                distance[i] = int.MaxValue;
                shortestPathTreeSet[i] = false;
            }

            distance[source] = 0;

            for (int count = 0; count < verticesCount - 1; ++count)
            {
                int u = MinimumDistance(distance, shortestPathTreeSet, verticesCount);
                shortestPathTreeSet[u] = true;

                for (int v = 0; v < verticesCount; ++v)
                    if (!shortestPathTreeSet[v] && Convert.ToBoolean(graph[u, v]) && distance[u] != int.MaxValue && distance[u] + graph[u, v] < distance[v])
                        distance[v] = distance[u] + graph[u, v];
            }

            Print(distance, verticesCount);
        }

        static void Main(string[] args)
        {
            int[,] graph =  {
                         { 0, 6, 0, 0, 0, 0, 0, 9, 0 },
                         { 6, 0, 9, 0, 0, 0, 0, 11, 0 },
                         { 0, 9, 0, 5, 0, 6, 0, 0, 2 },
                         { 0, 0, 5, 0, 9, 16, 0, 0, 0 },
                         { 0, 0, 0, 9, 0, 10, 0, 0, 0 },
                         { 0, 0, 6, 0, 10, 0, 2, 0, 0 },
                         { 0, 0, 0, 16, 0, 2, 0, 1, 6 },
                         { 9, 11, 0, 0, 0, 0, 1, 0, 5 },
                         { 0, 0, 2, 0, 0, 0, 6, 5, 0 }
                            };

            DijkstraAlgo(graph, 0, 9);
            Console.ReadKey();
        }
    }
}

نتیجه اجرا

Vertex    Distance from source
0         0
1         6
2         15
3         20
4         22
5         12
6         10
7         9
8         14

جهت استفاده سور رو قرار میدم

دانــــــلود سورس دایجسترا

برای ارسال نظر شما باید ابتدا وارد حساب کاربری خود شوید.